Eric Lengyel, Ph.D.

Eric Lengyel (pronounced LENG · el, with no Y) is the founder of Terathon Software. He holds a Ph.D. in Computer Science from the University of California, Davis, and a Masters Degree in Mathematics from Virginia Tech.

Eric is the creator of the following technologies:

The Slug library for GPU font rendering and typography.
The Transvoxel algorithm for multiresolution isosurface rendering.
The Open Game Engine Exchange (OpenGEX) file format.
The C4 Engine, a full-featured game engine.

Eric is the author of the book series Foundations of Game Engine Development, and he is the editor for the Game Engine Gems series. Over 20 years ago, he wrote the first book focused on mathematics in games, the best-selling Mathematics for 3D Game Programming & Computer Graphics. Eric has also been a long-time member of the editorial board for the Journal of Graphics Tools, and he has been a major contributor to the successful Game Programming Gems series.

Eric is an active researcher in the field of projective geometric algebra and recently authored the book Projective Geometric Algebra Illuminated. The educational resources that he has created for this subject can be found on projectivegeometricalgebra.org.

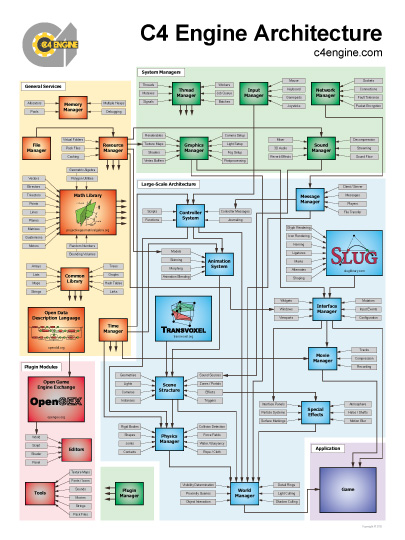
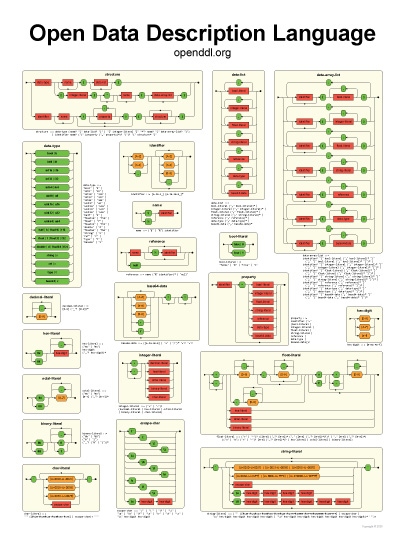
Eric previously worked in the advanced technology group at Naughty Dog and the graphics and imaging department at Apple. Before those, he was the lead programmer for the fifth installment of Sierra Studio’s popular RPG adventure series Quest for Glory. When he’s not at his desk, Eric can usually be found running somewhere in the mountains of northern California.

Eric’s email address is lengyel at this website’s domain.

Books

	Projective Geometric Algebra Illuminated Terathon Software, 2024 ISBN: 979-8985358254 projectivegeometricalgebra.org
	Foundations of Game Engine Development, Volume 1: Mathematics Terathon Software, 2016 ISBN: 978-0985811747 foundationsofgameenginedev.com
	Foundations of Game Engine Development, Volume 2: Rendering Terathon Software, 2019 ISBN: 978-0985811754 foundationsofgameenginedev.com
	Mathematics for 3D Game Programming & Computer Graphics, Third Edition Cengage Learning, 2011 ISBN: 978-1435458864 mathfor3dgameprogramming.com
	Game Engine Gems 1 Jones and Bartlett, 2010 ISBN: 978-0763778880 gameenginegems.com
	Game Engine Gems 2 A K Peters, 2011 ISBN: 978-1568814377 gameenginegems.com
	Game Engine Gems 3 A K Peters, 2016 ISBN: 978-1498755658 gameenginegems.com
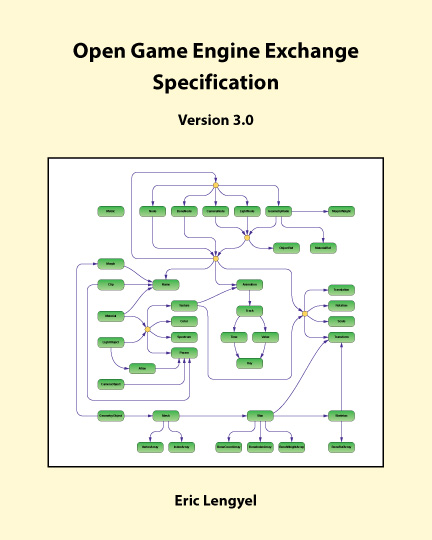	Open Game Engine Exchange Specification Terathon Software, 2013, 2015, 2017, 2021 ISBN: 978-0985811785 opengex.org
	Mathematical Concepts Introduction to Game Development, Second Edition Cengage Learning, 2011 ISBN: 978-1584506799
	Mathematics for 3D Game Programming & Computer Graphics, Second Edition Cengage Learning, 2003 ISBN: 978-1584502777 mathfor3dgameprogramming.com
	The OpenGL Extensions Guide Charles River Media, 2003 ISBN: 978-1584502944
	Mathematics for 3D Game Programming & Computer Graphics Cengage Learning, 2001 ISBN: 978-1584500377 mathfor3dgameprogramming.com

Papers and Gems

	GPU-Centered Font Rendering Directly from Glyph Outlines Journal of Computer Graphics Techniques Vol. 6, No. 2 Eric Lengyel, 2017 sluglibrary.com
	The Open Game Engine Exchange Format Game Engine Gems 3 Eric Lengyel, 2016 gameenginegems.com
	Fog with a Linear Density Function Game Engine Gems 3 Eric Lengyel, 2016 gameenginegems.com
	Smooth Horizon Mapping Game Engine Gems 3 Eric Lengyel, 2016 gameenginegems.com
	A Jitter-Tolerant Rigid Body Sleep Condition Game Engine Gems 2 Eric Lengyel, 2011 gameenginegems.com
	Bit Hacks for Games Game Engine Gems 2 Eric Lengyel, 2011 gameenginegems.com
	Motion Blur and the Velocity-Depth-Gradient Buffer Game Engine Gems 1 Eric Lengyel, 2010 gameenginegems.com
	Moments of Inertia for Common Shapes Game Engine Gems 1 Eric Lengyel, 2010 gameenginegems.com
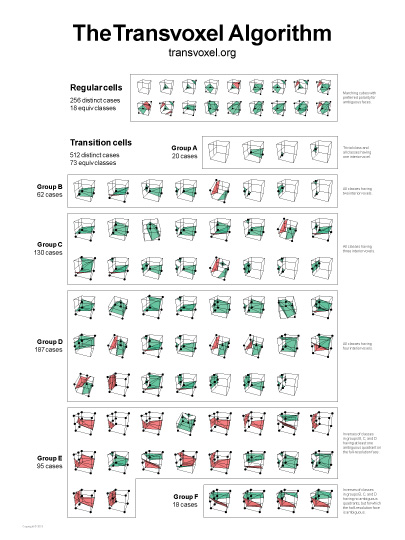
	Transition Cells for Dynamic Multiresolution Marching Cubes Journal of Graphics, GPU, and Game Tools Vol. 15, No. 2 Eric Lengyel, 2010 transvoxel.org
	Unified Distance Formulas for Halfspace Fog Journal of Graphics Tools Vol. 12, No. 2 Eric Lengyel, 2007
	On Faster Sphere-Box Overlap Testing Journal of Graphics Tools Vol. 12, No. 1 Thomas Larsson, Tomas Akenine-Möller, and Eric Lengyel, 2007
	Oblique View Frustums for Mirrors and Portals Game Programming Gems 5 Eric Lengyel, 2005
	Oblique Depth Projection and View Frustum Clipping Journal of Game Development Vol. 1, No. 2 Eric Lengyel, 2005
	T-Junction Elimination and Retriangulation Game Programming Gems 3 Best of Game Programming Gems Eric Lengyel, 2002
	The Mechanics of Robust Stencil Shadows Game Developer Eric Lengyel, 2002
	Applying Decals to Arbitrary Surfaces Game Programming Gems 2 Eric Lengyel, 2001
	Tweaking a Vertex’s Projected Depth Value Game Programming Gems Eric Lengyel, 2000
	A Fast Cylinder-Frustum Intersection Test Game Programming Gems Eric Lengyel, 2000
	Simultaneous Cross-Platform Game Development Game Developer Eric Lengyel, 2000
	3D Graphics Engine Essentials MacTech Magazine Vol. 15, No. 6 Eric Lengyel, 1999

Speaking

	An Overview of Game Engine Architecture Virginia Tech 2024 Blacksburg VA
	Geometry and Motion in Projective Exterior and Geometric Algebras Virginia Tech 2024 Blacksburg VA
	Optimizing Glyphs for Real-Time Vector Rendering Unicode Technology Workshop 2024 Sunnyvale CA
	Geometry and Motion in Projective Grassmann and Clifford Algebras Space Imaging Workshop Keynote 2024 Includes additional tutorial sessions Atlanta GA
	Projective Geometric Algebra and Rigid Transformations NASA 2024
	Foundations of Projective Geometric Algebra NASA Goddard Space Flight Center 2024 Greenbelt MD
	Practical Projective Geometric Algebra Game Developers Conference 2023 San Francisco CA
	New Developments in Projective Geometric Algebra Game Developers Conference 2021 San Francisco CA
	GPU-Centered Font Rendering Directly from Glyph Outlines Symposium on Interactive 3D Graphics and Games 2018 Montréal QC, Canada
	GPU Font Rendering: Current State of the Art Blizzard Seminar 2018 Irvine CA
	Linear Algebra Upgraded Game Developers Conference 2018 San Francisco CA
	Game Math Case Studies Game Developers Conference 2015 San Francisco CA
	Grassmann Algebra in Game Development Game Developers Conference 2014 San Francisco CA
	Fundamentals of Grassmann Algebra Game Developers Conference 2012 San Francisco CA
	A Bigger Mathematical Picture for Computer Graphics Winter School of Computer Graphics Keynote 2012 Plzeň, Czech Republic
	The Return of Forgotten Mathematics in Computer Graphics Freie Universität Berlin 2012 Berlin, Germany
	Evolution of a Game Engine McMaster University 2007 Hamilton ON, Canada
	Projection Matrix Tricks Game Developers Conference 2007 San Francisco CA
	Advanced Light and Shadow Culling Methods Game Developers Conference 2006 San Jose CA
	Advanced Stencil Shadow and Penumbral Wedge Rendering Game Developers Conference 2005 San Francisco CA

Informational Posters

	Binary Fundamentals Eric Lengyel, 2023 PDF • Print
	The Slug Algorithm Eric Lengyel, 2021 sluglibrary.com PDF • Print
	The C4 Engine Architecture Eric Lengyel, 2021 c4engine.com PDF • Print
	The Transvoxel Algorithm Eric Lengyel, 2018 transvoxel.org PDF • Print
	Open Data Description Language Eric Lengyel, 2020 openddl.org PDF • Print
	Projective Geometric Algebra Eric Lengyel, 2024 projectivegeometricalgebra.org PDF • Print
	Conformal Geometric Algebra Eric Lengyel, 2024 projectivegeometricalgebra.org PDF • Print